Assembly

The basic principle of the assembly process is the construction of a global stiffness matrix \(\boldsymbol{K}\) from the element stiffness matrices \(\boldsymbol{K}^{\mathrm{e}}\). In the following the procedure is outlined.

Consider the following mesh:

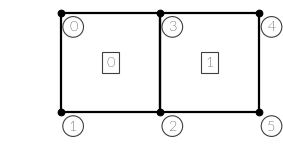
You could write it down in a node map like this:

element	node 0	node 1	node 2	node 3
0	0	1	2	3
1	1	4	5	2

Note

When you order your nodes on an element level, you have to do it consistently – either clockwise or counterclockwise!

You have one element stiffness matrix \(\boldsymbol{K}^{\mathrm{e}}\) for each element. It exists of several submatrices \(\boldsymbol{K}_{ij}^{\mathrm{e}}\) that take into account the interactions of node \(i\) with node \(j\).

\[\begin{split}\boldsymbol{K}^{\mathrm{e}} = \begin{bmatrix} \boldsymbol{K}_{00}^{\mathrm{e}} & \boldsymbol{K}_{01}^{\mathrm{e}} & \boldsymbol{K}_{02}^{\mathrm{e}} & \boldsymbol{K}_{03}^{\mathrm{e}} \\[1ex] \boldsymbol{K}_{10}^{\mathrm{e}} & \boldsymbol{K}_{11}^{\mathrm{e}} & \boldsymbol{K}_{12}^{\mathrm{e}} & \boldsymbol{K}_{13}^{\mathrm{e}} \\[1ex] \boldsymbol{K}_{20}^{\mathrm{e}} & \boldsymbol{K}_{21}^{\mathrm{e}} & \boldsymbol{K}_{22}^{\mathrm{e}} & \boldsymbol{K}_{23}^{\mathrm{e}} \\[1ex] \boldsymbol{K}_{30}^{\mathrm{e}} & \boldsymbol{K}_{31}^{\mathrm{e}} & \boldsymbol{K}_{32}^{\mathrm{e}} & \boldsymbol{K}_{33}^{\mathrm{e}} \end{bmatrix}\end{split}\]

The key to assembling the global stiffness matrix is to put the submatrices of the element stiffness matrix into the right position in the global stiffness matrix. For this you take one submatrix and look at the subscripts. Find the corresponding global indices and insert the submatrix at the corresponding position in the global stiffness matrix. In the simple mesh it looks like this:

\[\begin{split}\boldsymbol{K} = \begin{bmatrix} \boldsymbol{K}_{00}^0 & \boldsymbol{K}_{01}^0 & \boldsymbol{K}_{02}^0 & \boldsymbol{K}_{03}^0 & 0 & 0 \\[1ex] \boldsymbol{K}_{10}^0 & \boldsymbol{K}_{11}^0 + \boldsymbol{K}_{00}^1 & \boldsymbol{K}_{12}^0 + \boldsymbol{K}_{03}^1 & \boldsymbol{K}_{13}^0 & \boldsymbol{K}_{01}^1 & \boldsymbol{K}_{02}^1 \\[1ex] \boldsymbol{K}_{20}^0 & \boldsymbol{K}_{21}^0 + \boldsymbol{K}_{30}^1 & \boldsymbol{K}_{22}^0 + \boldsymbol{K}_{33}^1 & \boldsymbol{K}_{23}^0 & \boldsymbol{K}_{31}^1 & \boldsymbol{K}_{32}^1 \\[1ex] \boldsymbol{K}_{30}^0 & \boldsymbol{K}_{31}^0 & \boldsymbol{K}_{32}^0 & \boldsymbol{K}_{33}^0 & 0 & 0 \\[1ex] 0 & \boldsymbol{K}_{10}^1 & \boldsymbol{K}_{13}^1 & 0 & \boldsymbol{K}_{11}^1 & 0 \\[1ex] 0 & \boldsymbol{K}_{20}^1 & \boldsymbol{K}_{23}^1 & 0 & 0 & \boldsymbol{K}_{22}^1 \end{bmatrix}\end{split}\]

In our two dimensional linear elasticity problem each of those submatrices is a \(2 \times 2\) matrix as we have two degrees of freedom (DoF) on each node – displacement in \(x\)- and in displacement in \(y\)-direction.

For our implementation we follow the convention that the degrees of freedom are numerated according to the number of the node they are residing at:

Node	DoFs
0	0, 1
1	2, 3
2	4, 5
3	6, 7
4	8, 9
5	10, 11

With these ingredients you shoud be able to set up the assembly process!

System.assemble_stiffness_matrix()

Return the global stiffness matrix of the system.

Returns:The global stiffness matrix of the system. Return type:numpy.ndarray